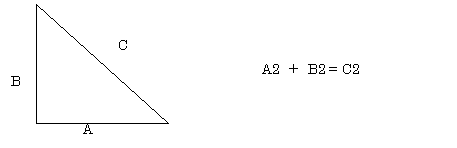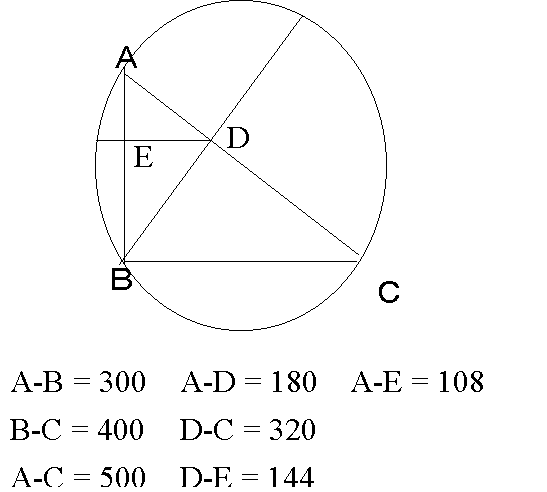The 47th
Problem of Euclid
by H. Meiji
Master, Harmony Lodge #18

 Portrait of Euclid according to
an old European etching
Portrait of Euclid according to
an old European etching
Introduction
There are so many symbols, words and
phrases in Freemasonry used both as part of its rituals as well as part of its
vocabulary, that studying and trying to understand the “meanings” them is a very
worthwhile and a rewarding journey. One such prominent symbol and phrase, is the
47th problem of Euclid, which is one of the main symbols introduced
in the Third Degree.
In the Blue Lodge, it is considered a great honor to be
elected and serve as the Master of a lodge. It shows that the individual has
attained maturity, leadership, charisma, and motivation, but above all,
knowledge to be able to lead others. It is an initiation by itself, as the
position brings with it a completely new set of responsibilities that are often
not appreciated when accepting the position. At the end of serving as Master of
a Lodge, many Past Masters are presented with a jewel, symbolizing the great
appreciation of the Lodge towards their dedication. It also symbolizes something
else ? that is that the individual has completed his “journey”, through the
different positions of the Lodge, to a new plain.
The 47th problem of Euclid features prominently in
many Past Master’s jewels. Selecting this symbol out of the thousands used in
Freemasonry to represent one of its highest honors must mean that it is a very
significant and central symbol of the Craft. Yet, sadly many Freemasons, even
many Past Masters, do not know why it is so centrally featured in the Past
Master’s jewel. Clearly the 47th problem is based on Geometry, and
all Freemasons know that Geometry and Freemasonry are closely linked, but is
this the only reason? What does the 47th problem of Euclid symbolize
and mean? Of the 465 problems published by Euclid, why is the 47th so
important? Why do Freemasons cherish it so?

(An example of a Past Master’s Jewel featuring the 47th
Problem of Euclid from England.
Past Master’s jewel used in the USA often do not show the 47th
Problem anymore)
The Foundation of
Freemasonry?
The 47th problem of Euclid is often mentioned in
Masonic publications. In Anderson's “Constitutions” published in 1723, it
mentions that “The Greater Pythagoras, provided the Author of the 47th
Proposition of Euclid's first Book, which, if duly observed, is the Foundation
of all Masonry, sacred, civil, and military…”. Being mentioned in one of the
first “official” speculative Masonic publications clearly indicates that the 47th
problem of Euclid must be important. It is also mentioned in the Third Degree
lecture, where we are taught that the “47TH problem of
Euclid…….taught us to be general lovers of the arts and sciences”.
However, it is quite different to be referred to as the
“Foundation of all Masonry, sacred, civil and military” that to be referred to
as “taught us to be general lovers of the arts and sciences”. Has the importance
of the symbolism of the 47th problem declined over time for some
reason?
In order to understand whether the symbol has declined in
importance or not, we first need to look at the 47th problem of
Euclid itself.
The Discovery of the
47th problem of Euclid
Euclid wrote a set of thirteen books, which were called
“Elements”. Each book contained many geometric propositions and explanations,
and in total Euclid published 465 problems. The 47th problem was set
out in Book 1, which is also known as “The Pythagorean Theorem”. Why is it
called by both these names? Although Euclid published the proposition, it was
Pythagoras who discovered it. We learn from the third degree lecture that:
"This wise philosopher (Pythagoras) enriched his mind
abundantly in a general knowledge of things, and more especially in Geometry,
or Masonry. On this subject he drew out many problems and theorems, and, among
the most distinguished, he erected this, when, in the joy of his heart, he
exclaimed Eureka, in the Greek language signifying, "I have found it," and
upon the discovery of which he is said to have sacrificed a hecatomb. It
teaches Masons to be general lovers of the arts and sciences."
Actually, it was not Pythagoras who directly discovered the
rule, as the Egyptians used the same principle for a very long time before
Pythagoras, whereby they re-measured their fields after the annual flooding of
the Nile washed out their boundary markers. Hence, Pythagoras is probably here
referred to as being the one who proved that the process works.
History records that Pythagoras
established a society with philosophical, religious and political aims. Shrouded
in secrecy, they believed that only by truly understanding the universe could
one achieve salvation of the soul, and as Divinity created all things, studying
it over a period of several lifetimes, could bring one closer to Divinity
itself. As such, it was believed that through study and reason could one start
to understand Divinity. Clearly, reason is based on measurable things (such as
through numbers and objects), and is easier to understand if expressed in that
matter. Hence the society devoted much of its time to the mathematics, including
Geometry. This line of thinking was incorporated in Freemasonry, which sets it
opposite to the Church, which emphasizes faith over reason. Indeed, Pope Pius
IX, in his encyclical, Qui Pluribus, dated 9 November 1846, attacked
those who “put human reason above faith, and who believe in human progress.”
Many people consider this to be a reference to Freemasonry.
This is interesting, because in the Book of Wisdom 11:20 we
read:
“Even apart from these, men could fall at a single
breath
when pursued by justice
and scattered by the breath of thy power.
But thou hast arranged all things by measure
and number and weight.”
So the very “measurement of things” the Church objects to is
mentioned in Scripture.
However, let us get back to how the 47th problem
fits in Freemasonry.
What Does the 47th
say?
The proposition states that: “In right angled triangles the
square on the side subtending the right angle is equal to the squares on the
sides containing the right angle.”
What? In other words A 2 + B2
= C2.
Many readers will feel like they have been returned to
Geometry class. A simple illustration will probably refresh our memories.
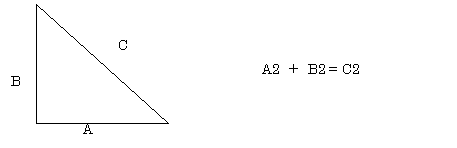
The proposition is especially important in architecture.
Builders have since ancient times used the theorem in constructing buildings by
a process known as “squaring a room.” As the theorem states that 3 squared + 4
squared = 5 squared, a builder starts by marking a spot and drawing a line, say
line A. This line is given the value of 3. The builder then marks another point,
say point B and draws a line from it at a right angle to line A, and it is given
the value of 4. The distance between line A and B is then measured, and if the
distance between A and B is 5, then the room is squared. By inverting the
process, a “squared” (or rectangle) room can be obtained.
Engineers who tunnel from both sides through a mountain use
the 47th problem to get the two shafts to meet in the center. The
surveyor who wants to know how high a mountain may be ascertains the answer
through the 47th problem. The astronomer who calculates the distance of the sun,
the moon, the planets, and who fixes "the duration of times and seasons, years,
and cycles," depends upon the 47th problem for his results. The navigator
traveling the trackless seas uses the 47th problem in determining his latitude,
his longitude, and his true time. Eclipses are predicted, tides are specified as
to height and time of occurrence, land is surveyed, roads run, shafts dug,
bridges built, with the 47th problem to show the way.
In some lodges, using this principle, a candidate
symbolically “squares the Lodge” by being escorted around the Lodge three times
during the Entered Apprentice ritual, four times for a Fellowcraft ritual, and
five times for a Master Mason ritual, which completed his journey.

(1738 German Drawing depicting workmen using the 47th
problem)
The 47th
problem forms the basis of all ancient measurement units
The 47th problem of Euclid formed the basis of a
common set of measurements used by the Egyptians, especially in the building of
the Great Pyramids. It gets a little technical, but a simple illustration will
help us understand it better.
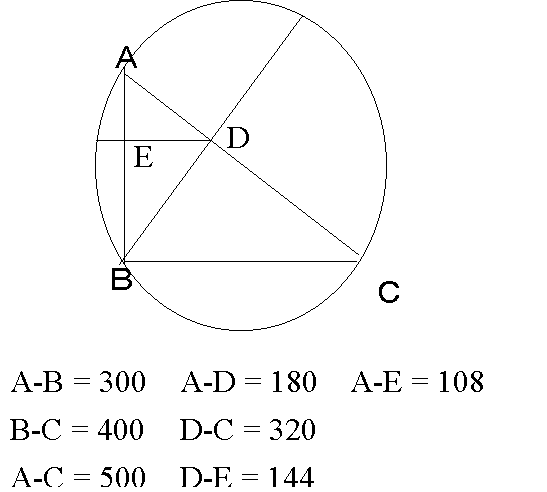
Please see the illustration above, which is
not accurate due to a drawing, but will serve to illustrate the point. If we
take a circle and draw in it a triangle (triangle A- B-C) which perpendicular is
300, base is 400, and by the 47th problem, the hypotenuse becomes 500
(any combination such as 3,4,5 will also work ? higher numbers are used for ease
of explanation). Then if we draw a line from the angle of the perpendicular and
the base through the hypotenuse to the circle, this line will be equal to 480.
The resulting two parts of the hypotenuse (A-D and D-C) will be equal to 180 and
320 respectively. Then if we draw another line from the point D (the intersector
of the hypotenuse) to the perpendicular of the shortest side of the triangle
(A-B), then line A-E will equal 108 and line D-E will equal 144.
Now we have all the measurements of the ancient world, that
is 500, 480, 400, 320, 180, 144 and 108. Why is this important? If we take each
unit to be a cubit (an ancient form of measurement), then 500 is the base of the
Great Pyramid of Memphis. 400 cubits is the length of an Egyptian stadium
(stadium is plural for stadia, and ancient measurement unit, based on a
particular number of steps, also called a Khet by the Egyptians). 480 cubits is
the length of the Ptolemy stadium, 320 cubits is the length of the Hebrew and
Babylonian stadium. Furthermore, 180, which represents the smaller part of the
hypotenuse, doubled gives 360 cubits, the Cleomedes stadium. By doubling 144
cubits gives 288 cubits, the Archimedes stadium. Finally by doubling 108 cubits
we obtain 216 cubits, or the lesser Egyptian stadium.
In other words, this simple exercise formed the basis of all
the lengths used by the Egyptians, and hence also once again indicates that its
principle was well understood by the Egyptians, and hence taught by them to
Pythagoras.
Conclusion
Clearly, the 47th problem helps us look at the
universe, and all that is in it, through a system that we can understand
clearly, for it is measurable. The Master’s jewel is the square, the base needed
for the 47th problem (in many jurisdictions the square has the
dimensions of 3:4 ? the Pythagorean dimensions). As the Master serves his
position, he becomes more complete, and therefore the 47th problem of
Euclid is dedicated on his jewel when he leaves office.
References
Circumambulation and Euclid’s 47th proposition, by
Reid McInvale
Encyclopedia of Freemasonry, by Albert Mackey
Freemasonry, A journey through ritual and symbol, by W. Kirk
Master Mason, by Carl Claudy
back to top |
![]()






 Portrait of Euclid according to
an old European etching
Portrait of Euclid according to
an old European etching